引 言
隨著電子產(chǎn)品日益輕薄短小、元件密度愈來愈高、工作速度愈來愈快,微流控系統(tǒng)得到了快速發(fā)展,其中微泵在藥物微量輸送、食品和化工定量灌裝、農(nóng)業(yè)育種試驗(yàn)、定量噴灑藥液或水霧、電子行業(yè)精準(zhǔn)定量點(diǎn)膠、集成電子元件冷卻、微量化學(xué)分析等*域得到廣泛應(yīng)用。
壓電泵是一種全新驅(qū)動(dòng)理論的新型微泵,它將傳統(tǒng)電磁泵的驅(qū)動(dòng)源部分、傳動(dòng)部分及泵體三者制成一體,不需附加驅(qū)動(dòng)電機(jī),具有體積小、質(zhì)量輕、不受電磁干擾等優(yōu)點(diǎn),已成為*內(nèi)外研究的熱點(diǎn)。1983 年荷蘭 Twente 大學(xué)將硅微加工與薄膜技術(shù)相結(jié)合研制出壓電泵
[1],韓*、德*、瑞士、美*等相繼研究開發(fā)了微型泵和微型閥
[2-19]。美*噴氣驅(qū)動(dòng)實(shí)驗(yàn)室利用與傳統(tǒng)行波馬達(dá)相似的原理為美**家航空和宇宙航行局研制出一種圓盤端面行波壓電
蠕動(dòng)泵。
中*清華大學(xué)在微流量系統(tǒng)和微流量方面做了大量
的研究工作
[20],吉林大學(xué)研制出矩形壓電振子式主動(dòng)閥壓電泵
[21-24],哈爾濱工業(yè)大學(xué)研制了壓電疊堆泵
[25],南
京航空航天大學(xué)
[26]和華南農(nóng)業(yè)大學(xué)等高校都對(duì)壓電泵進(jìn)行了相關(guān)的實(shí)驗(yàn)和理論研究
[27],并取得了很大進(jìn)展。
目前廣泛使用的
蠕動(dòng)泵通常為機(jī)械
蠕動(dòng)泵,主要由

收稿日期:2011-10-19 修訂日期:2012-04-05
項(xiàng)目基金:廣東省科技計(jì)劃項(xiàng)目(2010B020314003,粵科規(guī)劃字[2010]98 號(hào))作者簡介:梁 莉(1963-),女(漢),黑龍江人,**實(shí)驗(yàn)師,在讀博士生,華南農(nóng)業(yè)大學(xué)工程學(xué)院,研究方向?yàn)橹悄苻r(nóng)業(yè)機(jī)械,廣州 華南農(nóng)業(yè)大
學(xué)工程學(xué)院自動(dòng)化系,510642。Email: ll-scau@163.com
※通信作者:馬 旭(1959-),男(漢),黑龍江人,教授,博士,研究方向?yàn)檗r(nóng)業(yè)機(jī)械化。廣州 華南農(nóng)業(yè)大學(xué)工程學(xué)院農(nóng)業(yè)工程系,510642。
Email: maxu1959@scau.edu.cn

泵頭、電機(jī)、泵管組成,泵頭包括轉(zhuǎn)子和泵殼,泵管置于轉(zhuǎn)子與泵殼之間,電機(jī)作為驅(qū)動(dòng)器必不可少,因而增加了蠕動(dòng)泵的質(zhì)量和體積。
如前所述,有關(guān)壓電泵的研究主要集中于圓盤型驅(qū)動(dòng)振子面外振動(dòng)的壓電泵,而對(duì)于驅(qū)動(dòng)振子為圓盤型面內(nèi)周向行波振動(dòng)的壓電蠕動(dòng)泵研究則較少
[28-29]。
為此,本文將機(jī)械蠕動(dòng)泵結(jié)構(gòu)與壓電泵技術(shù)相結(jié)合,提出一種圓環(huán)型周向行波圓環(huán)型壓電蠕動(dòng)泵,旨在進(jìn)一步探索壓電技術(shù)在蠕動(dòng)泵中的應(yīng)用,減小蠕動(dòng)泵體積和質(zhì)量,簡化蠕動(dòng)泵結(jié)構(gòu),進(jìn)一步擴(kuò)大蠕動(dòng)泵的應(yīng)用*域。
1 圓環(huán)型壓電蠕動(dòng)泵結(jié)構(gòu)及工作機(jī)理
1.1 圓環(huán)型壓電蠕動(dòng)泵結(jié)構(gòu)
本文設(shè)計(jì)的圓環(huán)型壓電蠕動(dòng)泵結(jié)構(gòu)如圖 1 所示。
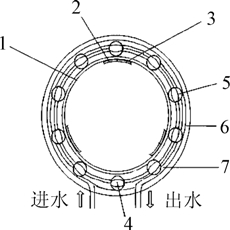
1.金屬彈性體內(nèi)圓環(huán) 2.壓電陶瓷片 A 區(qū) 3.壓電陶資片 B 區(qū) 4.滾柱固定
裝置 5.滾柱 6.金屬彈性體外圓環(huán) 7.硅管
圖 1 圓環(huán)型壓電蠕動(dòng)泵結(jié)構(gòu)圖
Fig.1 Structure of circular ring piezoelectric peristaltic pump
在金屬彈性體內(nèi)、外圓環(huán)材料均為硬鋁,軸向高度
15 mm,內(nèi)環(huán)外徑 38 mm,內(nèi)徑 32 mm,外環(huán)內(nèi)徑 42 mm,
通過之間夾有硅管,將極化并分為 A、B 區(qū)的矩形壓電陶瓷片沿金屬彈性體內(nèi)圓環(huán)內(nèi)側(cè)面均布粘接,其厚度為

1.2 mm,寬度 6 mm,長度 15 mm,構(gòu)成了圓環(huán)復(fù)合振子,在內(nèi)環(huán)外側(cè)面均布有短圓柱滾柱,為減輕質(zhì)量,選用尼龍材料滾柱。
1.2 圓環(huán)型壓電蠕動(dòng)泵工作原理
圓環(huán)型壓電振子以圓柱薄殼復(fù)合振子周向行波振動(dòng)模態(tài)代替機(jī)械蠕動(dòng)泵泵頭中的轉(zhuǎn)子擠壓硅管,省去電機(jī)驅(qū)動(dòng)裝置,減少了體積和質(zhì)量,工作原理如圖 2 所示。
在極化后的壓電陶瓷片 A 區(qū)和 B 區(qū)分別通以相位差為 90°、頻率和電壓幅值可調(diào)的交變電壓,由于壓電陶瓷材料的逆壓電效應(yīng),壓電陶瓷片產(chǎn)生交替形變,圓環(huán)型復(fù)合振子被激發(fā)出 2 個(gè)駐波,合成后在金屬彈性體外圓環(huán)產(chǎn)生周向行波,在周向預(yù)緊力作用下,振子沿圓周外表面行波通過尼龍滾柱不斷擠壓硅管,于是在內(nèi)圓環(huán)振子外圓周與外圓環(huán)內(nèi)圓環(huán)交界面上行波波峰之間就形成了多個(gè)腔體,腔體交替地形成與關(guān)閉將帶動(dòng)流體沿著波的行進(jìn)方向流動(dòng),管中流體受到推力,流體在此推力作用下沿圓周方向運(yùn)動(dòng),實(shí)現(xiàn)了蠕動(dòng)泵的效果。改變兩交流電壓相位差順序,流體沿圓周相反方向運(yùn)動(dòng)。在電壓幅值一定時(shí),改變頻率可以控制流體的流量和壓力。其工作原理如圖 2 所示。

式(3)~(5)中,
A、B 為曲面拉梅常數(shù);
E 為彈性模量,Pa;h 為金屬圓柱薄殼厚度,m;
ρ 為彈性體密度,kg/m
3;
g 為泊松比;
α、
β 分別為曲線坐標(biāo);
w 圓柱殼法線方向
的位移,m;
f 為圓柱殼法線方向的應(yīng)力函數(shù),Ñ
2 Ñ
2 為進(jìn)行二次拉普拉斯算子運(yùn)算。設(shè)
|
|
w(a , b , t ) = W (a , b )sin(wt + j) |
|
|
|
(6) |
|
|
f (a , b ,t ) = F (a , b )sin(wt + j) |
|
|
|
(7) |
|
則振型方程為 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DÑ2 Ñ 2W + Ñ 2 F - r hw2W = 0 |
|
|
|
(8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EhÑ |
2W - Ñ 2 Ñ 2 F = 0 |
|
|
|
|
|
|
|
|
|
|
(9) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對(duì)式(8)進(jìn)行Ñ2 Ñ2 運(yùn)算,對(duì)式(9)進(jìn)行Ñ |
2 運(yùn)算, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
然后相加,消去 F,可得關(guān)于 W 的 8 階齊次獨(dú)立方程 |
|
DÑ2 Ñ 2 Ñ 2 Ñ 2W + EhÑ 2 Ñ 2 FW - r hw 2 Ñ 2 Ñ 2W = 0 (10) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對(duì)于薄圓環(huán),取柱面坐標(biāo) α=x, β=θ,其拉梅常數(shù) A=1, |
|
B=R,主曲率半徑 Ra |
= ¥ , Rq |
= R ,則方程(10)中的算 |
|
子 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ 2 Ñ 2 = |
¶ 4 |
|
|
+ |
2 |
|
¶ 4 |
|
|
|
+ |
|
1 ¶4 |
|
|
|
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ x 4 |
|
R 2 ¶x 2 ¶q 2 |
|
R4 ¶q 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ |
2 Ñ |
2 |
|
= |
1 ¶4 |
|
|
|
|
|
|
|
|
|
|
(12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 ¶x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對(duì)封閉薄圓環(huán),設(shè)振型 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (x, q ) = Wn (x )cos nq |
|
|
|
(13) |
|
將式(11)、(12)、(13)代入式(10)得 |
|
|
D ( |
d 2 |
|
- |
|
n 2 |
)4W (x) + |
Eh d 4W (x) |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
dx |
|
|
|
R 2 |
R 2 |
|
|
|
dx4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
(14) |
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r hw |
( |
|
|
|
|
- |
|
|
|
|
) |
|
W (x) = 0 |
|
|
|
|
|
|
|
|
|
|
dx 2 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
設(shè)W (x ) = el x |
,代入式(14)得 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n 2 |
4 |
|
|
Eh |
|
|
4 |
|
|
|
|
|
2 |
|
|
2 |
|
n2 2 |
|
|
|
|
|
D[l |
- |
|
|
] |
|
+ |
|
R 2 |
|
l |
|
- r hw |
|
[l |
|
|
- |
|
] |
= 0 |
|
(15) |
|
|
R 2 |
|
|
|
|
|
|
|
R2 |
|
|
由式(15),得到 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
li = ± a1 , ± ia 2 , ± ( a3 |
|
+ ia4 ), ± ( a3 - ia4 ), |
|
|
|
(16) |
|
|
|
|
|
|
( j = 1, 2,3, 4,5,6,7,8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
從而可以得到 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wn (x ) = C1 sha1 x + C2 cha 1 x + C3 sina 2 x + C4 cosa2 x |
|
+ C ea 3 x sina |
x + C |
ea 3 x |
|
cosa |
x + C |
e -a3 x sina |
x |
|
|
5 |
|
|
|
4 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
7 |
|
|
|
|
4 |
|
|
|
+C e -a3 x |
cosa |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(17) |
|
8 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據(jù)薄圓環(huán)復(fù)合振子兩端的邊界條件可以建立關(guān)于待定系數(shù)
C1~
C8 的齊次線性代數(shù)方程組,由系數(shù)行列式為零,可得該復(fù)合振子的頻率方程及各階頻率與振型。
3 圓環(huán)型壓電蠕動(dòng)泵的有限元分析
圓環(huán)型壓電蠕動(dòng)泵是利用薄圓環(huán)復(fù)合振子在其周向

產(chǎn)生機(jī)械變形來擠壓膠管中的流體,薄圓環(huán)復(fù)合振子的材料特性對(duì)壓電蠕動(dòng)泵的工作性能**關(guān)重要。
根據(jù)生產(chǎn)廠家提供的壓電陶瓷 PZT-4,各獨(dú)立特性參數(shù)值見表 1。
表 1 壓電陶瓷 PZT-4 材料特性參數(shù)表
Table 1 Material characteristic parameters table of piezoelectric ceramic PZT-4

|
參數(shù) |
|
數(shù)值 |
|
|
|
|
|
|
C11 |
13.2 |
|
|
C12 |
7.10 |
|
彈性剛度系數(shù) CE/ |
C13 |
7.30 |
|
(1010 N·m-2) |
C33 |
11.5 |
|
|
|
|
C44 |
2.60 |
|
|
C66 |
3.00 |
|
|
|
|
|
|
d31 |
-123 |
|
壓電常數(shù) d/ |
d33 |
289 |
|
(10-12C·N-1) |
|
|
d15 |
496 |
|
|
|
|
|
介電常數(shù) ε/ |
ε11 |
1475 |
|
|
|
|
(8.85×10-12 F·m-1) |
ε13 |
1300 |
|
|
|
密度 ρp/(kg·m-3) |
|
7500 |

注:
Cij(
i=1, 3, 4, 6,
j=1, 2, 3, 4 ,6)為恒電場條件下的
j 向分量變化一個(gè)單位所引起的
i 向應(yīng)力分量的改變量。
金屬彈性體的內(nèi)、外圓環(huán)材料皆為硬鋁,密度為 2.7 ×10
3 kg/m
3 ,硬鋁的彈性模量為 70×10
9 Pa,泊松比
g 為0.33。當(dāng)壓電陶瓷參數(shù)和金屬彈性體內(nèi)外圓環(huán)材料參數(shù)確定后,改變薄圓環(huán)復(fù)合振子的內(nèi)、外徑及其高度等結(jié)構(gòu)參數(shù),通過對(duì)驅(qū)動(dòng)振子的振動(dòng)方程的分析和有限元數(shù)值計(jì)算得知,薄圓環(huán)復(fù)合振子的結(jié)構(gòu)參數(shù)改變,對(duì)其諧振頻率影響較大,適當(dāng)改變復(fù)合振子的結(jié)構(gòu)參數(shù),可以得到周向彎曲振動(dòng)模態(tài)的振型變化如圖 3 所示,其中圖 3a 和圖 3b 分別為同型近頻振型,諧振頻率分別為 1.6815、 1.6892 kHz,模態(tài)矢量的位移相對(duì)幅值分別為 10.491 和10.506。當(dāng)施加相差 90°、激勵(lì)頻率在 1.68~1.69 kHz 之
間時(shí),將激勵(lì)復(fù)合振子產(chǎn)生圖 2 所示的周向行波,驅(qū)動(dòng)流體產(chǎn)生蠕動(dòng)流動(dòng)。
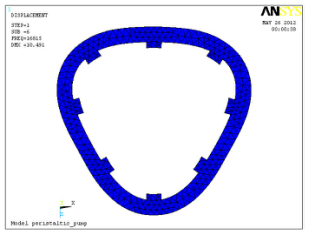
a. 驅(qū)動(dòng)振子振型 1

b. 驅(qū)動(dòng)振子振型 2
圖 3 驅(qū)動(dòng)振子振型有限元分析
Fig.3 Finite-element analysis of vibration shape of driven stator
由此可驗(yàn)證由振動(dòng)方程推導(dǎo)出的薄圓環(huán)復(fù)合振子的振動(dòng)為周向行波。
4 結(jié) 論
1)提出了一種圓環(huán)型壓電蠕動(dòng)泵的新型結(jié)構(gòu),其特點(diǎn)是以薄圓環(huán)復(fù)合振子為驅(qū)動(dòng)源;
2)由薄殼振動(dòng)理論推導(dǎo)出該復(fù)合振子的振動(dòng)方程,并可由此推導(dǎo)出周向行波產(chǎn)生的條件,對(duì)其加載相位差為 90°交變電壓所激發(fā)出的周向行波振動(dòng)模態(tài)能夠?qū)崿F(xiàn)對(duì)硅管內(nèi)流體的擠壓和虹吸作用,達(dá)到蠕動(dòng)效果;
3)改變交變電壓的頻率可以控制流體的流量和壓力,改變交變電壓相位順序可以改變流體流動(dòng)方向,諧振頻率為可操作頻率;
4)根據(jù)有限元分析軟件優(yōu)化設(shè)計(jì)出圓環(huán)型壓電蠕動(dòng)泵復(fù)合振子的振型。


